Формы геометрических тел
Деталь любой формы можно представить как совокупность отдельных геометрических тел.
Для примера возьмем деталь (рис. 159. а) и проанализируем се форму. Мысленно разделив ее на отдельные элементы, получим следующие геометрические тела (рис. 159, б): 1 — усеченный прямой круговой конус с цилиндрическим отверстием, 2 — прямой круговой цилиндр, 3 — прямоугольный параллелепипед, 4 — два прямоугольных параллелепипеда с цилиндрическими отверстиями, 5 — два полых полуцилиндра. Для выполнения комплексных чертежей необходимо усвоить методы проецирования отдельных геометрических тел, а также точек и линий, расположенных на поверхности этих тел.
Рис. 159
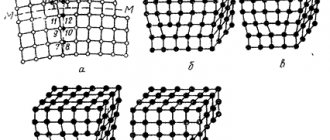
Геометрические тела, ограниченные плоскими многоугольниками, называются многогранниками (рис. 160, а). Эти многоугольники называются гранями, их пересечения — ребрами. Угол, образованный гранями, сходящимися в одной точке — вершине, называется многогранным углом.
Тела вращения ограничены поверхностями, которые получаются в результате вращения какой-либо линии вокруг неподвижной оси (рис. 160, б и в). Линия АВ, которая при своем движении образует поверхность, называется образующей. Наиболее часто встречаются такие тела вращения, как цилиндр, конус, шар, тор.
Рис. 160
Рисование шара
Геометрическая форма шара самая простая из всех фигур, но для рисунка шар является самым сложным заданием. В первую очередь, начинающим сложно нарисовать ровный круг, трудно добиться плавных тональных переходов при штриховке, чтобы шар на рисунке не имел вмятин. Шар можно осветить естественным светом от окна или мягким светом с рассеивателем. Такой свет лучше, он не даёт резких теней.
При освещении лампой накаливания контраст сильнее, часто это приводит к тому, что начинающие изображают шар слишком тёмным, как будто он не из гипса, а из свинца.
Ниже представлен готовый рисунок шара. Изображения поэтапного ведения работы, построения теней, объяснения природы рефлексов появятся на сайте позже.
После того, как освоен рисунок геометрических тел по отдельности, можно приступить к рисованию группы из геометрических тел. Как правило, композиция включает в себя куб или параллелепипед, 1-2 тела вращения и шар. Рисунок кувшина также выполняется после того, как ученик умеет изображать простые геометрические формы.
Разрешено копирование статей, только при наличии активной (кликабельной) ссылки на страницу-источник сайта Дениса Гаврилова gavrilovart.ru и при указании авторства. Ссылка должна находиться непосредственно рядом с материалом, должна быть видимой и прямой (без использования java-скриптов). Запрещено каким-либо образом изменять, затирать, отрезать копирайты на копируемых с моего сайта фотографиях или иллюстрациях.
Проекции призм
Построение проекций правильной прямой шестиугольной призмы (рис. 161) начинается с выполнения ее горизонтальной проекции — правильного шестиугольника. Из вершин этого шестиугольника провопят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Эта проекция изображается отрезком горизонтальной прямой. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер — отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых. Передняя боковая грань 1243 изображается на плоскости V без искажения, а на плоскости W— в виде прямой линии. Фронтальные и профильные проекции остальных боковых граней изображаются с искажением.
На чертеже оси х, у и z не показывают, что делает чертеж более простым.
Рис. 161
Несколько сложнее построение проекций наклонной призмы.
Рассмотрим порядок построения проекций наклонной шестиугольной призмы.
1. Призма, основание которой лежит на плоскости Н, наклонена к этой плоскости под утлом α (рис. 162, а). Ребра призмы параллельны плоскости V, т.е. являются фронталями.
Вначале выполняется построение горизонтальной проекции основания призмы, которое проецируется на плоскость Н без искажения (правильный шестиугольник). Фронтальная проекция основания представляет собой отрезок прямой, параллельной оси х.
Из точек 1′, 2′, 3′ фронтальной проекции основания проводят прямые проекции ребер под углом α к оси х и на них откладывают действительную длину бокового ребра призмы.
Строят фронтальную проекцию верхнего основания призмы в виде отрезка прямой, равного и параллельного фронтальной проекции нижнего основания.
Из точек 1, 2, 3, 4. 5. 6 горизонтальной проекции нижнего основания проводят прямые — проекции ребер — параллельно оси х и на них с помощью вертикальных линий связи находят шесть точек — горизонтальные проекции вершин верхнего основания призмы.
2. Прямая правильная шестиугольная призма наклонена под углом α к плоскости Н. Основание призмы наклонено к плоскости Н под углом β (рис. 162, б).
В этом случае необходимо вначале построить фронтальную проекцию основания. Эта проекция представляет собой отрезок, равный расстоянию между параллельными сторонами шестиугольника. Если этот отрезок разделить пополам и из его середины провести линию связи, то на ней будут расположены точки 2 и 5 — горизонтальные проекции вершин основания призмы. Расстояние между точками 2, 5 равно действительному расстоянию между вершинами основания призмы. Так как горизонтальные проекции сторон 16 и 34 представляют собой их действительные длины, то, воспользовавшись этим обстоятельством, можно построить полностью горизонтальную проекцию основания.
Дальнейший процесс построения, показанный на рис. 162, б, аналогичен приведенному на рис. 162, а.
Рис. 162
На комплексных чертежах предметов часто приходится строить проекции линий и точек, расположенных на поверхности этих тел, имея только одну проекцию линии или точки. Рассмотрим решение такой задачи.
Дан комплексный чертеж четырехугольной прямой призмы и фронтальная проекция а’ точки А.
Прежде всего надо отыскать на комплексном чертеже две проекции грани, на которой расположена точка А. На комплексном чертеже видно (рис. 163, а), что точка А лежит на грани призмы 1265. Фронтальная проекция а’ точки А лежит на фронтальной проекции 1’2’6’5‘ грани призмы. Горизонтальная проекция 1562 этой грани — отрезок 56. На этом отрезке и находится горизонтальная проекция а точки А. Профильную проекцию призмы и точки А строят, применяя линии связи.
По имеющемуся комплексному чертежу призмы можно выполнить ее изометрическую проекцию по координатам вершин. Для этого вначале строят нижнее основание призмы (рис. 163, б), а затем вертикальные ребра и верхнее основание (рис. 163, в).
По координатам т и п точки А, взятым с комплексного чертежа, можно построить аксонометрическую проекцию этой точки.
Рис. 163
Коническая поверхность вращения
Оглавление:
Коническая поверхность вращения
Прямой круговой конус
Коническая поверхность вращения — это линейчатая поверхность, образованная вращением прямолинейной образующей, которая пересекает криво-линейную направляющую (окружность) и проходит через неподвижную точку оси вращения, называемую вершиной.
Конусом называют геометрическое тело, ограниченное конической поверхностью и плоскостью основания, пересекающего все его образующие.
Конус называют прямым, если ось вращения перпендикулярна его основанию. Конус называют круговым, так как направляющей является окружность Конус с двумя параллельными основаниями, т.е. конус со срезанной вершиной, называют усеченным.
Построение проекций прямого кругового конуса
На рис. 4.71 показан пример построения проекций прямою кругового конуса с горизонтально-проецирующей осью вращения , заданной высотой и основанием радиусом .
Для построения проекций конуса требуется выполнить графо-аналитические действия в следующем порядке:
1-е действие. По заданному условию построить горизонтальную проекцию очерка прямого кругового конуса, которая представляет собой окружность заданного радиуса с вершиной , совпадающей с осью вращения .
2-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса:
- Круг радиуса является невидимой проекцией основания конуса.
- Круг радиуса с вершиной конуса является видимой проекцией боковой поверхности конуса.
- Обозначить на горизонтальной проекции характерные образующие конуса и которые будут определять очерки фронтальной и профильной проекций конуса.
3-е действие. Построить фронтальную проекцию (очерк) конуса, которая представляет собой треугольник заданной высоты , ограниченный:
- слева и справа — проекциями боковых очерковых образующих и ;
- горизонтальным отрезком , который является проекцией основания конуса;
- фронтальными проекциями характерных образующих и , которые совпадают с осью конуса .
4-е действие. Построить профильную проекцию (очерк) конуса:
- ‘Задать на окружности горизонтальной проекции конуса положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности.
- Выбрать положение базовой оси (б.о.), которая будет совпадать с вертикальной осью вращения на профильной проекции конуса.
- Профильная проекция конуса представляет собой треугольник ограниченный:
слева и справа очерковыми образующими и построенными по координате :
вершиной , лежащей на базовой оси ; горизонтальным отрезком проекцией основания;
профильными проекциями характерных образующих и , которые совпадают с осью вращения конуса .
!!! Запомните характерные признаки очерков прямого круговою конуса на чертеже — окружность основания и два треугольника.
!!! Характерные признаки очерков прямого кругового усеченного конуса окружность основания и две равнобокие трапеции.
Построение проекции точек, лежащих на поверхности конуса
Принадлежность точки поверхности конуса определяется ее принадлежностью образующей поверхности и принадлежностью круговым параллелям (окружностям), по которой точка вращается вокруг оси конуса. Следовательно, проекции точки можно строить либо по принадлежности образующей, либо по принадлежности круговой параллели.
На рис. 4.71 показан пример построения горизонтальных и профильных проекций точек и , заданных фронтальными проекциям и но их принадлежности круговым параллелям.
Посфоение горизонтальных проекций заданных точек:
- горизонтальная проекция характерной точки , лежащей на характерной образующей конуса , определяется на горизонтальной проекции этой образующей;
горизонтальные проекции точек и построены на вспомогательных круговых параллелях, проведенных через заданные фронтальные проекции точек.
Рассмотрим графический алгоритм для построения горизонтальных проекции точек, лежащих на боковой поверхности конуса (на примере заданной точки , по их при надежности круговым параллелям:
Графический алгоритм I:
1-е действие. Провести фронтальную проекцию вспомогательной круговой параллели через заданную фронтальную проекцию точки : проекция параллели — это прямая, перпендикулярная оси конуса и параллельная его основанию.
2-е действие. Провести окружность горизонтальной проекции параллели полученным радиусом .
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки на горизонтальной проекции параллели
Повторить действия графического алгоритма 1 и построить аналогично горизонтальные проекции и точек и .
Построение профильных проекций заданных точек. Точки и построены по принадлежности характерным образующим:
точка лежит на видимой характерной образующей , совпадающей с осью конуса;
- точка лежит на характерной образующей .
- точки и построены по координатам .
- точка — по координате (видимая);
- точка — по координате (невидимая).
На рис. 4.72 показан пример построения горизонтальной и профильной проекции точки по ее принадлежности образующей .
- Построение горизонтальной проекции точки по принадлежности образующей выполняется по графическому алгоритму II:
1-е действие. Провести через вершину конуса и заданную невидимую фронтальную проекцию точки вспомогательную образующую
2-е действие. Построить горизонтальную проекцию образующей проходящей через вершину конуса и вспомогательную точку , лежащую на основании конуса.
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки по ее принадлежности образующей .
- Построение профильной проекции невидимой точки выполняется по принадлежности образующей , построенной но координате .
На рис. 4.72 показано построение фронтальной и профильной проекции точки по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
1-е действие. Провести на горизонтальной проекции конуса радиусом окружность вспомогательной параллели или вспомогательную образующую , на которых лежит горизонтальная проекция точки .
2-е действие. Построить фронтальные проекции вспомогательной параллели или вспомогательной образующей :
параллель провести через вспомогательную точку на образующей параллельно основанию конуса;
образующую провести через вспомогательную точку на основании конуса и вершину конуса
3-е действие. Построить по вертикальной линии связи фронтальную проекцию точки по ее принадлежности либо параллели , либо образующей .
Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся):
1-й случаи. Гели секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим (фронтально-проецирующая плоскость , рис. 4.73).
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность но окружности (горизонтальная плоскость рис. 4.73).
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость параллельна одной образующей , рис.4.74).
4-и случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость параллельна двум образующим — и , рис.4.75).
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе, не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость ), рис 4.76).
Рассмотрим построение на проекциях конуса линии пересечения для всех пяти случаев сечений.
1-й и 2-й случаи. На рис. 4.73 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью , проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью , расположенной перпендикулярно оси конуса (2-й случай).
Плоскость пересекает поверхность конуса по образующим , горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки лежащей на основании конуса.
Плоскость пересекает поверхность конуса по окружности радиуса ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 4.74 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью , расположенной параллельно одной образующей конуса .
Плоскость пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена)
Построение проекций этих точек выполнено по их принадлежности:
- точка лежит на проекциях характерной образующей ;
- точки лежат на проекциях характерных образующих и , горизонтальные проекции которых построены с помощью параллели радиусом (алгоритм I);
- точки лежат на окружности основания конуса: горизонтальные проекции этих точек определяются по линии связи на горизонтальной проекции окружности основания, а их профильные проекции построены по координате ,
- проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате ).
Оформление очерков проекций видно из чертежа.
4-й случай. На рис. 4.75 показано построение проекций конуса со срезом фронтальной плоскостью , расположенной параллельно двум образующим конуса и .
Плоскость пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 1. 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза
Оформление очерков проекций видно из чертежа.
На рис 4 75 на профильной проекции конуса показано положение секущей плоскости под углом к оси конуса. При плоскость пересекает поверхность конуса также по гиперболе.
5-й ыучай. На рис. 4.76 показано построение проекции конуса со срезом фронтально-проецирующей плоскостью пересекающей все образующие конуса под углом к оси, отличным от прямого.
Плоскость пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 и про-межуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Почки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции но координате (алгоритм I).
Оформление очерков проекций видно из чертежа.
!!! Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построении проекции прямого конуса со срезами плоскостями частного положения
На рис. 4.77 показан пример построения проекций прямого круговою конуса со срезами фронтально-проецирующей плоскостью и профильной плоскостью .
Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания и высоте фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью и профильной плоскостью ;
2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выпол-иить графический анализ сечений:
1. Фронтально-проецирующая плоскость параллельна одной образующей конуса и пересекает его поверхность по участку параболы , которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения плоскостей срезов и .
- Профильная плоскость параллельна двум образующим конуса и и пересекает его поверхность по участку гиперболы , которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов и и плоскости с основанием конуса (4-4).
3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
1. Плоскость среза определяет видимая горизонтальная проекция участка параболы построенной по горизонтальным проекциям обозначенных точек:
- точка лежит на образующей ;
- точки и построены по принадлежности соответствующим параллелям (алгоритм I).
- Плоскость среза определяет вертикальный видимый отрезок вырожденной в линию проекции профильной плоскости, точки которой лежат на очерковой окружности основания конуса.
!!! Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура:
- Горизонтальный очерк определяют участок окружности и отрезок .
- Внутренний контур определяет видимый участок параболы .
5-е действие. Достроить профильную проекцию конуса со срезами, пост-роив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
1. Плоскость среза а определяет видимый участок параболы , построенный по профильным проекциям обозначенных точек:
- точка лежит на характерной образующей
- точки лежат соответственно на характерных образующих и ;
- точки построены по координате .
- Плоскость среза определяют видимые участки гиперболы , ограниченные видимым отрезком (построен) и видимым отрезком . точки которого построены но координате .
6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
- Профильный очерк определяют:
- слева — участок образующей :
- справа — участок образующей ;
- сверху — участок параболы ;
- снизу — проекция основания конуса.
- Внутренний контур определяют:
- видимые участки параболы ;
- видимый отрезок пересечения плоскостей срезов и ; видимые участки гиперболы .
7-е действие. Оформить чертеж конуса, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Эта теория взята со страницы задач по начертательной геометрии:
- Решение задач по начертательной геометрии
Возможно эти страницы вам будут полезны:
| Построение проекций пирамиды со срезами плоскостями частного положения |
| Построение проекций цилиндра со срезами и плоскостями частного положения |
| Построение проекции точек па поверхности шара |
| Построение проекции тара со срезами плоскостями частного положения |
Проекции пирамид
Построение проекций треугольной пирамиды начинается с построения основания, горизонтальная проекция которого представляет собой треугольник без искажения (рис. 164, а). фронтальная проекция основания — отрезок горизонтальной прямой.
Из горизонтальной проекции точки s (вершины. пирамиды) проводят вертикальную линию связи, на которой от оси х откладывают высоту пирамиды и получают фронтальную проекцию s’ вершины. Соединяя точку s’ с точками 1′, 2′ и 3′, получают фронтальные проекции ребер пирамиды.
Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки s с горизонтальными проекциями точек 1, 2 и 3.
Пусть, например, дана фронтальная проекция а’ точки А, расположенной на грани пирамиды 1s2, и требуется найти другую проекцию этой точки. Для решения этой задачи проведем через а’ произвольную вспомогательную прямую и продолжим ее до пересечения с фронтальными проекциями 1’s’ и 2’s’ ребер в точках п’ и т‘. Затем проведем из точек п’ и т‘ линии связи до пересечения с горизонтальными проекциями 1s и 2s этих ребер в точках п и т. Соединив п с т, получим горизонтальную проекцию вспомогательной прямой, на которой с помощью линии связи найдем искомую горизонтальную проекцию а точки А Профильную проекцию этой точки находят по линиям связи.
Другой способ решения задачи на построение проекции точки по заданной ее проекции показан на рис. 164, б. Дана четырехугольная правильная пирамида. Через заданную фронтальную проекцию а’ точки А проводят вспомогательную прямую, проходящую через вершину пирамиды и расположенную на ее грани. Горизонтальную проекцию ns вспомогательной прямой находят с помощью линии связи. Искомая горизонтальная проекция а точки А находится на пересечении линии связи, проведенной из точки а’, с горизонтальной проекцией ns вспомогательной прямой.
Фронтальная диметрическая проекция рассматриваемой пирамиды выполняется следующим образом (рис. 164, в).
Вначале строят основание, для чего по оси х откладывают длину диагонали 13, а по оси у — половину длины диагонали 24. Из точки О пересечения диагоналей проводят ось z и на ней откладывают высоту пирамиды. Вершину S соединяют с вершинами основания прямыми линиями — ребрами.
Фронтальную диметрическую проекцию точки А, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чертежа. От качала координат О по оси х откладывают координату xА, из се конца параллельно оси у — половину координаты yА и из конца этой координаты параллельно оси z — третью координату zА. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х откладывают координату xB и из конца ее проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.
Рис. 164
Проекции цилиндров
Боковая поверхность прямого кругового цилиндра получается вращением отрезка АВ образующей вокруг оси, параллельной этому отрезку. На рис. 165, а представлена изометрическая проекция цилиндра.
Построение горизонтальной и фронтальной проекций цилиндра показано на рис. 165, б и в.
Построение начинают с изображения основания цилиндра, т.е. двух проекций окружности (рис. 165, б). Так как окружность расположена на плоскости Н, то она проецируется на эту плоскость без искажения. Фронтальная проекция окружности представляет собой отрезок горизонтальной прямой линии, равный диаметру окружности основания.
После построения основания на фронтальной проекции проводят две очерковые (крайние) образующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, который является фронтальной проекцией верхнего основания цилиндра (рис. 165, в).
Рис. 165
Определение недостающих проекции точек А и В, расположенных на поверхности цилиндра, по заданным фронтальным проекциям в данном случае затруднений нс вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность (рис. 166. а). Следовательно, горизонтальные проекции точек А и В можно найти, проводя из данных точек а’ и b’ вертикальные линии связи до их пересечения с окружностью в искомых точках а и Ь.
Профильные проекции точек А и В строят также с помощью вертикальных и горизонтальных линий связи.
Изометрическую проекцию цилиндра вычерчивают, как показано на рис. 166, б.
В изометрии точки A и В строят по координатам. Например, для построения точки В от начала координат О по оси х откладывают координату xB = n, а затем через ее конец проводят прямую, параллельную оси у, до пересечения с контуром основания в точке 1. Из этой точки параллельно оси x проводят прямую, на которой откладывают координату xB = h1 точки В.
Рис. 166
Создание ассоциативных чертежей цилиндра и конуса
Процесс создания ассоциативных чертежей цилиндра и конуса, такой же как и призмы, и пирамиды. Поэтому детали я опущу, подробнее о построении можете прочитать здесь — Как создать ассоциативный чертеж по 3d модели и найти проекции точек на пирамиде и призме?
Хочу только отметить следующее. Вы уже успели заметить, что созданные виды на чертеже, находятся в проекционной связи, т. е. перемещать их можно только вдоль границ главного вида. И только, начав перемещение главного вида, можно сдвинуть вверх или вниз и остальные.
комплексный (ассоциативный) чертеж цилиндра
Для того чтобы получить возможность перемещать каждый вид по отдельности нужно отменить проекционную связь. Для этого нажимаем левой кнопкой мыши по габаритному прямоугольнику вида (при этом, он подсветится зеленым), затем правой кнопкой вызываем контекстное меню и снимаем выделение с команды «Проекционная связь».
Проекции конусов
Нагляднее изображение прямого кругового конуса показано на рис. 167, а. Боковая поверхность конуса получена вращением отрезка BS вокруг оси, пересекающей отрезок в точке S. Последовательность построения двух проекций конуса показана на рис. 167, б и в. Сначала строят две проекции основания. Горизонтальная проекция основания — окружность. Фронтальной проекцией будет отрезок горизонтальной прямой, равный диаметру этой окружности (рис. 167, б). На фронтальной проекции из середины основания восставляют перпендикуляр и на нем откладывают высоту конуса (рис. 167, в). Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и получают фронтальную проекцию конуса.
Рис. 167
Если на поверхности конуса задана одна проекция точки А (например, фронтальная проекция на рис. 168, а). то две другие проекции этой точки определяют с помощью вспомогательных линий — образующей, расположенной на поверхности конуса и проведенной через точку А, или окружности, расположенной в плоскости, параллельной основанию конуса.
В первом случае (рис 168. а) проводят фронтальную проекцию s’a’f ’ вспомогательной образующей. Пользуясь вертикальной линией связи, проведенной из точки f, расположенной на фронтальной проекции окружности основания, находят горизонтальную проекцию sf этой образующей, на которой с помощью линии связи, проходящей через а’, находят искомую точку а.
Во втором случае (рис. 168. б) вспомогательной линией, проходящей через точку А, будет окружность. расположенная на конической поверхности и параллельная плоскости Н. Фронтальная проекция этой окружности изображается в виде отрезка Ь’с’ горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция а точки А находится на пересечении линии связи, опущенной из точки а’, с горизонтальной проекцией вспомогательной окружности.
Если заданная фронтальная проекция Ь’ точки В расположена на контурной (очерковой) образующей SK, то горизонтальная проекция точки находится без вспомогательных линий (рис. 168. б).
В изометрической проекции точку А, находящуюся на поверхности конуса, строят по трем координатам (рис. 168, в): xА = n, yА = m, zА = h. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата xА = n; из конца ее параллельно оси у проведена прямая, на которой отложена координата yА = m; из конца отрезка, равного т, параллельно оси z проведена прямая, на которой отложена координата zА = h. В результате построений получим искомую точку А.
Рис. 168
Круглый конус в геометрии
Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.
Вам будет интересно:Юридический колледж в Иваново: специальности, приемная комиссия, отзывы
Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.
Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.
Вам будет интересно:Термофильные бактерии: польза и вред для человека
Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.
Проекции шара
На рис. 169, а изображена половина шара, сферическая поверхность этого шара образована вращением четверти окружности АВ вокруг радиуса АО.
Проекции этой фигуры приведены на рис. 169, б. Горизонтальная проекция — окружность радиуса, равного радиусу сферы, а фронтальная — полуокружность того же радиуса.
Если точка А расположена на сферической поверхности (рис. 169, в), то вспомогательная линия Ь’с’, проведенная через эту точку параллельно горизонтальной плоскости проекций, проецируется на горизонтальную плоскость проекций окружностью. На горизонтальной проекции вспомогательной окружности находят с помощью линии связи искомую горизонтальную проекцию а точки А.
Величина диаметра вспомогательной окружности равна фронтальной проекции Ь’с’.
Рис. 169
Получение фигуры с помощью вращения
Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.
Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c — это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.
Очевидно, что катет a будет радиусом основания фигуры, катет b — его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.
Проекции кольца и тора
Поверхность кругового кольца (рис. 170, а) образована вращением образующей окружности ABCD вокруг оси ОО1.
Тор — поверхность, образованная вращением части дуги окружности, являющейся образующей, вокруг оси ОО1, расположенной в плоскости этой окружности и не проходящей через ее центр.
Рис. 170
На рис. 171, а и б приведены два вида тора. В первом случае образующая дуга окружности радиуса R отстоит от оси вращения на расстоянии меньше радиуса R, а во втором случае — больше.
В обоих случаях фронтальные проекции тора представляют собой действительный вид двух образующих дуг окружности радиуса R, расположенных симметрично относительно фронтальной проекции оси вращения. Профильными проекциями тора будут окружности.
Круговое кольцо (или открытый тор) имеет горизонтальную проекцию в виде двух концентрических окружностей, разность радиусов которых равна толщине кольца или диаметру образующей окружности (рис. 170, б). Фронтальная проекция ограничивается справа и слева дугами полуокружностей диаметра образующей окружности.
Рис. 171
В случае, когда точка А лежит на поверхности кругового кольца и дана одна се проекция, для нахождения второй проекции этой точки применяется вспомогательная окружность, проходящая через данную точку А и расположенная на поверхности кольца в плоскости, перпендикулярной оси кольца (рис. 172).
Если задана фронтальная проекция а’ точки А, лежащей на поверхности кольца, то для нахождения ее второй проекции (в данном случае — профильной) через а’ проводят фронтальную проекцию вспомогательной окружности — отрезок вертикальной прямой линии b’c’. Затем строят профильную проекцию b»с» этой окружности и на ней, применяя линию связи, находят точку а“.
Если задана профильная проекция а» точки D, расположенной на поверхности этого кольца, то для нахождения фронтальной проекции точки D через d» проводят профильную проекцию вспомогательной окружности радиуса O»d“. Затем через верхнюю и нижнюю точки е» f» этой окружности проводят горизонтальные линии связи до пересечения с фронтальными проекциями образующей окружности радиуса r и получают точки e’ и f’. Эти точки соединяют вертикальной прямой, которая представляет собой фронтальную проекцию вспомогательной окружности (она будет невидима). Проводя горизонтальную линию связи из точки d» до пересечения с прямой e’f ‘, получаем искомую точку d’.
Такие же приемы построения применимы и для точек, находящихся на поверхности тора.
Рис. 172
Учимся рисовать правильные пропорциональные конусы
Конус лежит в основе многих предметов: елей, многих духовых инструментов, рупоров, абажуров ламп и так далее. Поэтому так важно освоить эту фигуру на начальных этапах курсов по рисунку. Кроме того, геометрические фигуры помогают начинающему художнику понять законы перспективы и научиться показывать объем на рисунке.
Рисование геометрических фигур – одна из составляющих программы всех художественных школ. Без умения изображать их не может обойтись ни один художник, независимо от того, в каком стиле он собирается работать в дальнейшем. Обычно курс начинается именно с них, а уже потом ученики переходят к более сложным материалам – к рисунку розеток, капителей, лиц и фигур людей. Каждый художник также должен легко накладывать штриховку при помощи карандаша и создавать объем.
Если вы собираетесь поступать в художественный вуз, вам предстоит сдавать творческий экзамен. Изображение геометрического тела – это одно из его заданий. Несмотря на видимую простоту рисования конуса, изобразить его с первой попытки без ошибок получается далеко не у всех. Поэтому будет лучше, если перед вступительными испытаниями вы достаточно потренируетесь. Для успешной сдачи абитуриентам нужно изобразить не одно тело вращения и отточить свое мастерство, чтобы на самом испытании чувствовать себя уверенно и свободно.
Школа-студия «Мастер рисунка» К. Э. Арутюновой уже не первый год готовит абитуриентов к поступлению в главные художественные вузы Москвы. Рисованию геометрических фигур, тел вращения отводится на курсах достаточно времени. К каждому ученику здесь применяется индивидуальный подход с учетом его уровня подготовки и количества времени до экзамена. Преподаватель отмечает все ошибки учащегося и доступно объясняет их, дает советы по исправлению. Запишитесь на курсы по телефону или через форму на сайте.